輪胎系統是乘用車的重要組成部分。德國大陸汽車、Polytec和戴姆勒公司密切合作,共同分析了E-class車前輪軸上的輪胎系統的三維振動。利用有限元方法建立滾動輪胎的數學模型,并與車輛模型耦合。本次試驗使用Polytec公司的三維掃描式激光多普勒測振儀對整車NVH性能進行測試,并驗證模型的有效性。
高復雜性:一個輪胎含有20多個部件
輪胎系統的主要功能是為了支撐車重,并在加速、剎車和轉彎時,將力傳遞到路面上。此外,它還負責減少因不規則路面所帶來的振動和噪聲,提高乘客的乘坐舒適性。隨著內燃機的噪聲降低、新的驅動系統的出現、及車輛零部件的輕量化,輪胎系統的第二功能變得越來越重要。
除了對輪胎的噪聲、振動和聲振粗糙度(NVH)性能的要求越來越高之外,降低開發成本和時間的需求也日益迫切,我們需要精確有效的數值方法來輔助開發過程。
由于若干因素,對輪胎系統的理解和數學建模極具有挑戰性。首先,雖然輪胎的外胎、輪輞和內腔可以被認為是兩種固體結構和一種封閉的流體,但僅外胎就含有20多個部件。每個部件由一個或多個非線性材料組成,其性能取決于溫度、應變率、應變幅值和應變史。其次,輪胎的激勵發生在與路面的接觸處,因此是路面形狀與外胎在接觸面的非線性動態響應函數。
對于振幅較小以及頻率在20 ~ 400Hz之間的,可以使用模態模型來有效地描述輪胎響應。基于輪胎阻尼的復雜分布、滾動產生的回轉力以及輪胎內外胎-輪輞與空腔之間的耦合等因素,滾動輪胎系統一般采用最通用的模態模型。
本次試驗中,在車輛單輪上加上受控運動激勵。三維掃描式激光多普勒測振儀加上合理位置擺放的反射鏡,可以測量旋轉輪胎大部分可見表面。振幅的精確測量不僅可以幫助加深理解系統的動態特性,還可以驗證復雜的數學模型和預測結果。
數學模型
根據結構質量矩陣Ms、結構剛度矩陣Ks、流體質量矩陣Mf、流體剛度矩陣Kf,從有限元模型來引出結構的物理特性。由于氣腔與結構之間的耦合作用(使用Hsf矩陣來描述),系統矩陣呈非對稱性[1]。在對車輪進行非線性靜力加載和滾動后使用任意拉格朗日-歐拉法(ALE),運動方程可表示為式(1)
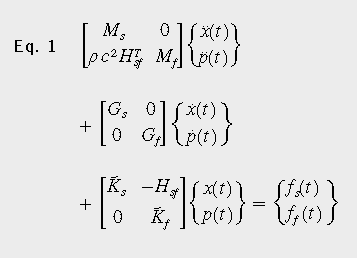
這里,ρ為空氣密度,c是聲速,Gs是結構的反對稱陀螺矩陣,Gf是流體的反對稱陀螺矩陣。時變量分別為位移x、聲壓p和力f。
為得到標準特征值形式[2],需要根據式2(a)和2(b)將式1中的N×N二階微分方程, 變換成2N×2N一階微分方程。
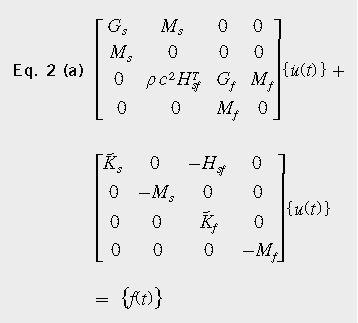
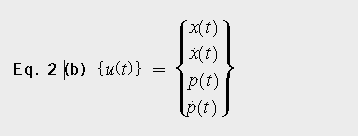
由于方程式2中的非對稱性矩陣,本征解將包含單一特征值矩陣[sr]和兩組復雜的特征向量[ΘLH]和[ΘRH]。右邊的特征向量(RH)描述模態振型,左邊的特征向量(LH)描述激勵振型。復模態不僅具有與實模態相同的振幅,而且還具有相位,以行波的形式出現;這與用駐波可更好地描述的實模態形成了對比。
輪轂的邊界條件描述
車輪與車輛子結構的耦合可以通過空間模型、模態模型或響應模型來實現。本文采用后一種方法來計算車輪與車輛的耦合振動響應。耦合響應方法是建立在兩個子結構共有界面的自由度的相容性和平衡條件的基礎上。通過位移導納方法,由[HA]和[HB]兩個非耦合FRF矩陣計算出耦合FRF矩陣[HC],如方程式3所示:
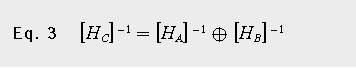
車輪子結構的位移導納,即單位力下的位移量,由模態模型計算得出。這種響應方法的一個優點是,由于輪輞和輪轂之間的耦合點需要的自由度很少,因此變換后的矩陣非常簡潔,如方程3所示。

圖1 所測車輛有限元模型,底盤上約有200萬個節點
圖1 顯示的是本次實驗所用的車輛有限元模型,包括底盤細節(大約200萬個節點)、動力總成和完整的車身結構(大約500萬個節點)。
通過計算輪轂在六個方向上的位移導納矩陣F/X,獲得用于輪胎與車輛連接的36個頻響函數(FRF)。通過輪轂中心到底盤或車身點可進一步計算出頻率響應函數。
測試裝置
如圖2所示,大陸汽車公司的試驗臺使用了Polytec公司的3D掃描式激光多普勒測振儀[3,4]。右前輪胎置于轉鼓上。

圖2 左側為3D掃描式激光測振儀,右側為轉鼓試驗臺
滾筒表面做了輕微不均勻性處理,并施加一個已知的激勵并確保輪胎和轉鼓始終保持接觸。在有限的頻率集下,對輪胎的每一速度施加一定頻率范圍的運動激勵,頻率與轉鼓轉速成正比。
車輪由轉鼓驅動,速度恒定在33至99km/h之間(3km/h為速度增加步長)。在每個恒定速度上,從9個不同的角度掃描車輪,其中四個不同角度是來自于車輪后方的反射鏡。
為獲取三維振動工作響應向量,使用三個不同測量方向的掃描頭進行振動測試。測振系統的光學頭探測到輪胎表面沿著激光方向上的多普勒頻移,這與其瞬時振動速度成正比。通過坐標變換,獲取振動矢量的x、y和z分量。通過三束激光同步掃描,可以測量包括相位在內的振動特性。
測試結果
車輪的響應,或者說車內噪聲,很大程度上是由輪胎的前幾階模態所決定。這些模態振型在軸上產生很大的合力,通常是一階模態,即一階左右平動模態、一階上下平動模態、一階空腔諧振模態等。
在測量滾輪的過程中,記錄了駕駛艙內四個位置的聲壓級。在300Hz以下,可以很容易地識別這些信號的頻譜峰值,以及相應頻率下車輪的工作變形(ODS),如圖3所示。可以預料的是,很多這樣的點都是由ODS變形導致的。

圖3 90 km/h時的胎面變形
滾動輪胎系統的ODS可以在測得頻率計算得出。為此,首先使用響應耦合法計算出輪軸之間界面自由度上的力。然后將這些力與接觸處的運動激勵一起應用于模態輪胎模型。這樣,可將車輪表面振動特性的計算值和測量值進行比對。
表1顯示的是同位移比例下,計算和測量出的幾個重要的輪胎響應的ODS結果的對比。不同顏色代表不同的瞬時速度。令人高興的是,我們可以看到在速度最高99km/h的范圍內,計算出來的ODS都可以通過測試得到相同的結果。旋轉的關鍵之處[5,6]在試驗和計算中都在控制之內。
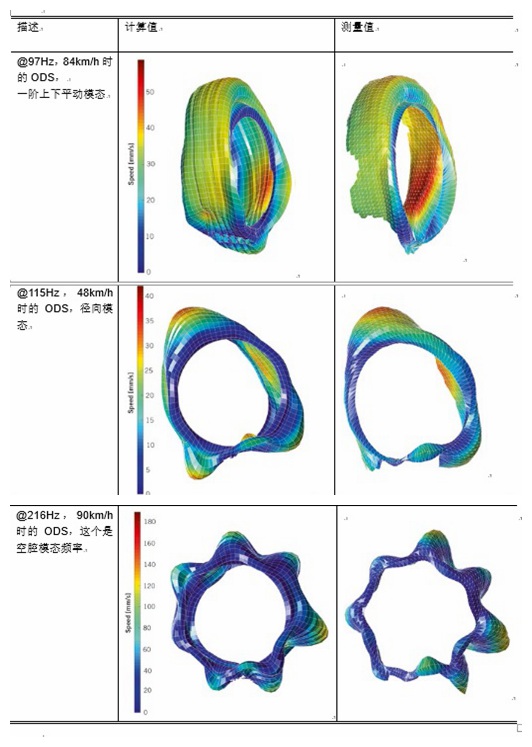
表1 幾個頻率下計算和測量的ODS對比
總結和展望
本文采用創新的非接觸式激光測振技術結合先進的輪胎和車輛模型,對輪胎滾動噪聲和振動進行了詳盡的研究。試驗結果表明,盡管這兩個領域的科研均具有挑戰性,但計算結果和測量結果具有很好的一致性。
本研究使用的輪胎模型僅根據設計參數而建立,并沒有使用輪胎物理數據。在研發過程,輪胎在正式投入生產前需要數字預測,而激光測振儀可以提供大量高質量測試數據對模擬數據進行驗證,促進模型的進一步升級。同時,測得結果還能幫助用戶更好地理解滾動輪胎的機械性能,在大量輪胎樣品測試的基礎上,使用與本文相同的測試方法,可驗證仿真的質量,這是開發早期階段的數字方法的基礎,可提升車輪與車輛的NVH性能。
鳴謝
本項目得到Ingo Busch、戴姆勒公司車身&底盤NVH測試部門、以及德國大陸汽車公司輪胎力學和NVH工程部門的Achillefs Tsotras博士和Diogo Baptista博士等的大力支持,感謝所有相關方的合作和支持。